ANALISIS DE FOURIER

Utilizando el análisis de Fourier y la transformada de Fourier se pueden describir formas de ondas más complejas como las que producen los instrumentos musicales.

Descripción
A primera vista, parece que el problema de analizar formas de ondas complejas representa una tarea formidable. Sin embargo, si la forma de la onda es periódica, se puede representar con una precisión arbitraria, mediante la superposición de un número suficientemente grande de ondas senoidales que forman una serie armónica. Se puede representar en forma de una suma infinita de funciones armónicas, es decir,

El applet nos permite elegir entre cuatro tipo de funciones discontinuas que representan pulsos periódicos.

• Rectangular
• Doble escalón
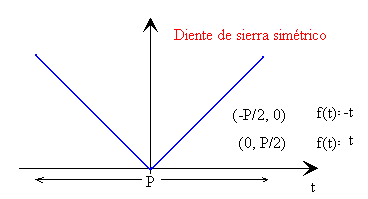
• Diente de sierra simétrico
• Diente de sierra antisimétrico

Una vez elegido la función, introducimos los parámetros requeridos en los controles de edición y pulsamos el botón cuyo título da nombre a la función.

• Rectangular
• Doble escalón
• Diente de sierra 1
• Diente de sierra 2

Pulsando sucesivamente en el botón titulado Siguiente >> se representa:

1. En la parte superior, la función f(t) elegida y las sucesivas aproximaciones de dicha función.

2. En la parte central, el armónico actual, en color azul a_i·cos(ix) y en color rojo b_i sin(ix).

3. En la parte inferior, mediante segmentos verticales, la magnitud relativa de los coeficientes de Fourier, a la izquierda en color azul los coeficientes a_i, y a la derecha en color rojo los coeficientes b_i.

Ejemplos

Pulso rectangular

El pulso rectangular nos permite verificar que son nulos los coeficientes b_i en una función cuya simetría es par. Probar el siguiente ejemplo: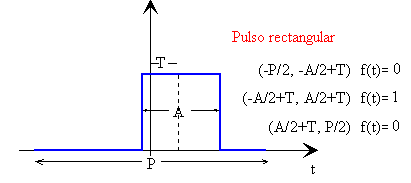

• Periodo, 5.0
• Anchura, 2.0
• Traslación, 0.0.

Pulso doble escalón
El pulso doble escalón nos permite verificar que son nulos los coeficientes a_i en una función cuya simetría es impar. Probar el siguiente ejemplo:
 

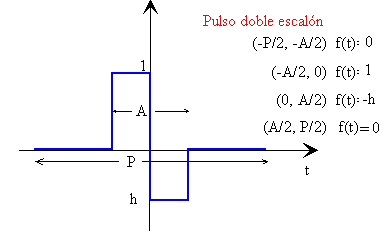
• Periodo, 3.0
• Anchura, 2.0
• Profundidad, 1.0.

Si cambiamos la profundidad del escalón derecho, la función deja de tener simetría y por tanto, aparecen coeficientes a_i y b_i. Probar el siguiente ejemplo:

• Periodo, 3.0
• Anchura, 2.0
• Profundidad, 0.5.

 Pulso diente de sierra simétrico